View a grid of CalabiYau Shapes View a Spinning CalabiYau Shape String Theory predicts the existence of more than the 3 space dimensions and 1 time dimension we are all familiar with⾒たカラビ・ヤウ多様体について探っていきます. <表紙CGコメント> 今⽉号の表紙の絵は複素 2 次元ユークリッド空間において,x^5 y^5 = 1 で定義される超曲⾯を実 3 次元に射影し,メッシ ュ化したものです.これはフェルマー 5 次超曲⾯と呼ばれており,これを⾼次元化した代数多様体はカラビ・ヤウ多様体 カラビ・ヤウ多様体の概要 ナビゲーションに移動検索に移動原文と比べた結果、この記事には多数(少なくとも 5 個以上)の誤訳があることが判明しています。情報の利用には注意してください。正確な語句に改訳できる方を求めています。
物質波が正弦波である仕組み
カラビ ヤウ 空間
カラビ ヤウ 空間-Candelas et al (1985)では、"カラビ・ヤウ空間"と呼ばれた。最初は微分幾何学の立場から、エウゲニオ・カラビE Calabi (1954, 1957)で研究され、シン=トゥン・ヤウが、これらがリッチ平坦(、リッチ曲率が 0 であるリーマン多様体である1 カラビヤウ多様体のある族と潜在的保型性 —佐藤テイト予想の証明に向けて— 原隆 (Takashi Hara)∗ 08年10月17日 概要 HSBT に従って,GSpnガロワ表現に対する潜在的モジュラー性定理及び、その佐藤テイト予想への応 用について概説する。 この文章は,08 年3 月に行われた『R = T



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ
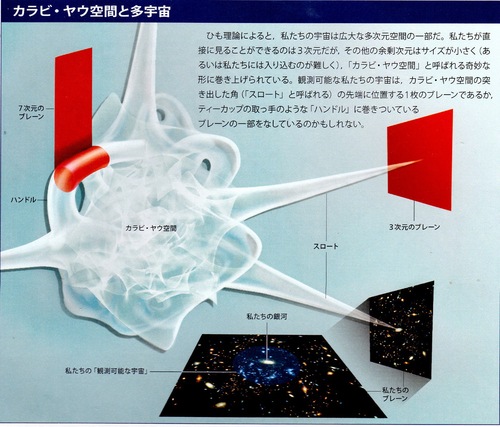
3次元カラビヤウ多様体は非常に小さく縮こまった (あるいはコンパクト化された)余分な空間の次元を定 義するものと考えられる。カラビヤウ多様体によるコ ンパクト化は1984年にフィリップ・元空間をコンパクト化することが必要である。こう して得られる4 次元理論の性質は6 次元の内部空間 の性質に大きく依存している。特に近年、ゲージ場 のフラックスがその上にあるようなカラビ・ヤウ空間 によるコンパクト化が素粒子模型として有望であるカラビ-ヤウ空間の図なのですが、 これって、脳みそに似ているな~と思いました。 そもそも「カラビ-ヤウ多様体」ってなんじゃらほい?という話なのですが、これがまたウィキペディアの「カラビヤウ多様体」の項目 を何回読んでもさっぱり分からなかったりします(恥) カラビヤウ
ヤウ多様体 の用例・例文集 これらのモデルは、リーマン面から普通はカラビヤウ多様体である固定された対象空間上への写像に関係する。このことはシンプレクティック多様体は一般化された複素多様体であるのみならず、さらに一般化されたカラビヤウ多様体であることを意味する。エウジェニオ・カラビ(伊 Eugenio Calabi 、1923年 5月11日 )は、イタリア王国 ミラノ出身の イタリア系アメリカ人 数学者。 ペンシルベニア大学の名誉教授であり、研究分野は微分幾何学、偏微分方程式である。 カラビヤウ空間を微分幾何学の立場から研究したためカラビ予想の由来にもなり31/01/ · カラビ・ヤウ多様体(英CalabiYau manifold)は、代数幾何などの数学の諸分野や数理物理で注目を浴びている特別なタイプの多様体 である。 特に 超弦理論 では、時空の 余剰次元 が6 次元 (実 次元 )のカラビ・ヤウ 多様体 の形をしていると予想されている。
することができる。具体的にはアーベル多様体、カラビ・ヤウ多様体、などのモジ ュライ空間を扱うが、これらの多様体は数理物理でも現われる多様体であり、その 性質を調べておくことは重要である。 当該研究課題と関連の深い論文・著書 ・TKatsura and FOort, Familiesカラビ=ヤウ空間ピカレスクさんのユーザーページです。存在と真実における世のあらすじ 褒められもせず、苦にもされない存在 ニコニコ 動画;いまや宇宙論には欠かせない「カラビ=ヤウ多様体」の生みの親であるヤウが、自らの数奇な半生と「見えざる」次元の幾何学への熱い想いを、多数の図版と平易な解説とともに語り尽くす。 Previous page 本の長さ 400ページ 言語 日本語 出版社 岩波書店 発売日 12/3/28 ISBN10 ISBN13



Calabi Yau多様体をブラウザ上に可視化する Three Js Sw1227 S Diary



小林晋平 これは担任した学生たちから記念にもらったカラビ ヤウ多様体のオブジェ こんなのが売ってるとは むちゃくちゃ気に入ってます Http T Co Ewnsbaqpx9
キーワード:カラビ・ヤウ多様体,ミラー対称性 現在の研究概要 カラビ・ヤウ多様体のミラー対称性について研究しています. 複素ケーラー多様体で接束の第1チャーン類が自明な多様体はカラビ・ヤウ 多様体と呼ばれ,数学・理論物理学の両面から関心が持たれ研究されています.特 にカラビヤウ空間を見てみよう! とね日記 学び カテゴリーの変更を依頼 記事元 bloggoonejp/ktonegaw 適切な情報に変更 エントリーの編集 エントリーの編集は 全ユーザーに共通 の機能です。 必ずガイドラインを一読の上ご利用ください。 タイトル ガイドライン キャンセル 保存する このⅠ カラビ・ヤウ空間 c理論(キャットバード理論)は、「カラビ・ヤウ空間」を設定している。 「カラビ・ヤウ空間」とは、「対称性」を保ったまま、9次元の空間の内6次元の空間がコンパクト化したものだ。 残った空間の3つの次元には、それぞれコンパクト化した2つの次元が付いている



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ



Terubumi Honjou Researchmap
「カラビ・ヤウ空間が 3つの穴を持っていると、3つの振動パターンの世代ができ、粒子の 3世代は実験的に観察されるであろう。 論理的には、弦の振動はすべての次元を通して巻き付く数を変化させるので、それらの振動数や、従って観察される基本粒子の性質に影響を与えるであろう。ニコニコについて サービス一覧 rss(更新情報)一覧 動画・生放送に使用できる音源の検索 宣言 サイトヤウ どういたしまして。 細野 超弦理論のカラビ‐ヤウ 多様体のことを考えると、私は 先生は宇宙での最重要人物のお 一人とも言えると思います。 では、まずこの特別な多様体 に興味を持たれたのはなぜかと いうことからお聞きしたいと思 います。ここに先生の著書の The Shape of Inner Space



ホログラフィック宇宙


カラビ ヤウ空間 竹内薫の はじめての数式処理ソフト より Maxima で綴る数学の旅
カラビ‐ヤウ空間 ここ1か月以上、カラビ‐ヤウ空間に逃げ込んでいました。 この宇宙が何でできているかそれを追求する物理学者たちの研究のなかで、この仮説は生まれました。私たちが当たり前のことと認識している3次元の空間と時間、合わせて4次の時空ではなく、10次あるいは11カラビ・ヤウ空間は非常に小さく、人間にはとても知覚できない。また非常に複雑で難解な空間で、多くの謎に満ちていると言われています オプティマル エアリ セブンは、部屋に設置するだけで、10次元空間をつくりだし 人の理解を超えた世界にアクセスできる製品です。 ではもし仮に「カラビ=ヤウ多様体」という数学的に美しい幾何学模様に魅せられて、ついつい「E8理論」と呼ばれる理論の「幾何学的美しさ」に心を動かされてしまいました。 ここでまた、カラビ=ヤウ多様体に戻って、数回に分けて「ミラー対称性」と「T双体性」について記述します。 M理論 「次元と



重力波でパラレルワールドは発見できるか Back To The Past



Calabi Yau多様体をブラウザ上に可視化する Three Js Sw1227 S Diary
Candelas et al (1985)では、"カラビ・ヤウ空間"と呼ばれました。 最初は微分幾何学の立場から、エウゲニオ・カラビE Calabi (1954, 1957)で研究され、シン=トゥン・ヤウが、これらが「リッチ平坦」注* な計量を持つであろうというカラビ予想を証明したことから、カラビ・ヤウ多様体と命名されカラビ予想 カラビヤウ多様体 主な受賞歴 パットナムフェロー (英語版) (1946年) スティール賞(1991年) プロジェクト人物伝 テンプレートを表示 ペンシルベニア大学の名誉教授であり、研究分野は微分幾何学、偏微分方程式である。 カラビヤウ空間を微分幾何学の立場から研究した



数学科 学習院大学 理学部 学習院大学大学院 自然科学研究科


3



量子的世界像 101の新知識 ケネス フォード とね日記



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ



至高のフラッシュ 4 4 Nogi Note



カラビ ヤウ空間 Classic音楽 リュート 宇宙



ひもに隠れた カラビ ヤウ多様体 とは その2 真実を求めて go go


統一理論への道 第3回 1 超弦理論からm理論の登場へ ヤスコヴィッチのぽれぽれblog



Rpga1069 システィーナ インタビュー記録 J どうも先生 今回はカチュウについて教えていただけますか D 勿論だとも ゴホン この時代 素粒子物理学の急速な発展により カラビ ヤウ空間理論が立証されたことにより 人類は遂に カラビ



オプティマル アリア ゼロ



科学雑誌ニュートン 17年11月号 ニュートンプレス



聖書に啓示されている超弦理論とダークマター Idle Utterance


美しい数学的な解 カラビ ヤウ多様体 2 未来に向かって ブログtoto



日本科学未来館 7月新登場の 未来館 サイエンスtシャツ3種 その1つ カラビ ヤウ多様体 をご紹介 Facebook



Tatsuki Hayama 巴山竜来 Artworks サイエンス社 数理科学 18年10月号


宇宙の法 を握る幾何 カラビ ヤウ多様体 2 未来に向かって ブログtoto



ミラー対称性 弦理論 Wikiwand



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ



Rpga1069 システィーナ インタビュー記録 J どうも先生 今回はカチュウについて教えていただけますか D 勿論だとも ゴホン この時代 素粒子物理学の急速な発展により カラビ ヤウ空間理論が立証されたことにより 人類は遂に カラビ


1


物質波が正弦波である仕組み



10次元までの世界を段階的に徹底解説 6次元で全宇宙にアクセス 7次元でもう1つの宇宙へ 高次元世界のすべて



物理学 数学の動画 相対性理論 量子論 電磁気学 超弦理論など とね日記



小林晋平 これは担任した学生たちから記念にもらったカラビ ヤウ多様体のオブジェ こんなのが売ってるとは むちゃくちゃ気に入ってます Http T Co Ewnsbaqpx9



宇宙の法を握る カラビ ヤウ多様体 真実を求めて go go



統一理論への道 第2回 3 超弦理論 隠された次元 ヤスコヴィッチのぽれぽれblog



カラビ ヤウ多様体って ワープする宇宙 より 成功と幸福を手に入れるヒント



10次元までの世界を段階的に徹底解説 6次元で全宇宙にアクセス 7次元でもう1つの宇宙へ 高次元世界のすべて 17年11月29日 エキサイトニュース



カラビ ヤウ多様体 Calabi Yau Manifold Japaneseclass Jp



カラビ ヤウ空間を見てみよう とね日記



Calabi Yau多様体をブラウザ上に可視化する Three Js Sw1227 S Diary
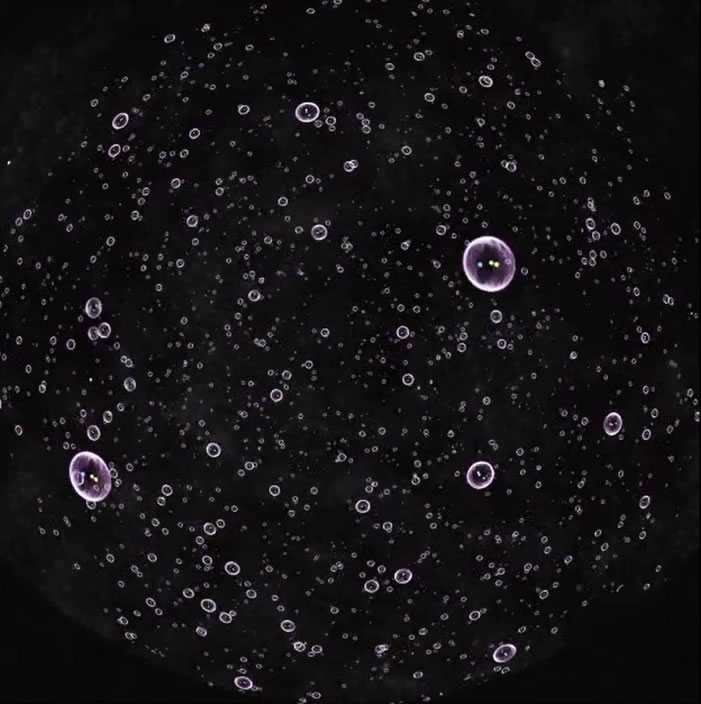


9次元から来た男とは何者か 9次元からきた男 日本科学未来館



9次元の世界へようこそ 超弦理論 が映像に 量子力学と相対性理論を統合する 万物の理論 とは 4 5 Jbpress Japan Business Press
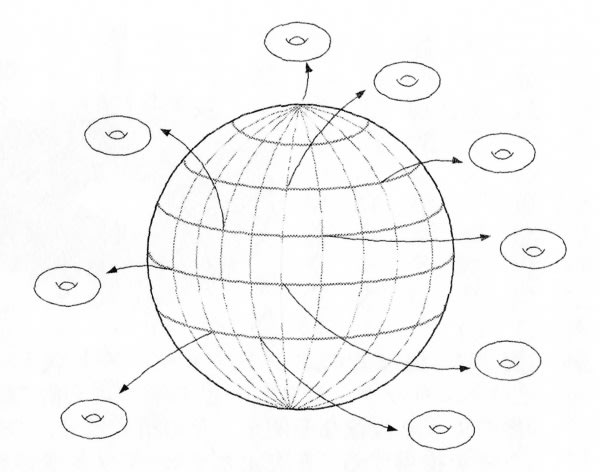


t双体性のtはトーラス 真実を求めて go go


物理学 テーマ カラビ ヤウ多様体 クラインの壺 の画像素材 イラスト素材ならイメージナビ



Calabi Yau多様体をブラウザ上に可視化する Three Js Sw1227 S Diary



ミラー対称性 弦理論 Wikiwand



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ


カラビヤウ空間 Applestar 宇宙と猫の部屋



カラビ ヤウ多様体 Calabi Yau Manifolds Tigerのブログ


理科散歩 本の森へ Ssブログ



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ



9次元から来た男とは何者か 9次元からきた男 日本科学未来館



10次元をイラストにすると 超弦理論も解説 オカルトオンライン



夢の徒然 扉の向こう側 山屋の一日


Q Tbn And9gcthq Z5uri8pcczjsjlnmxefsvoupe0blj6qj 8zz02whjdzneo Usqp Cau


Www Ipmu Jp Sites Default Files Webfm Pdfs News21 J Feature Pdf



カラビヤウ空間 Applestar 宇宙と猫の部屋
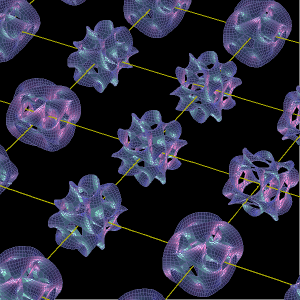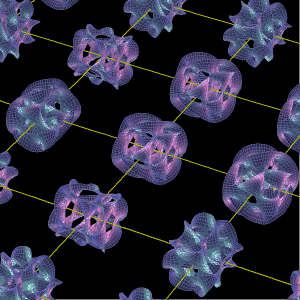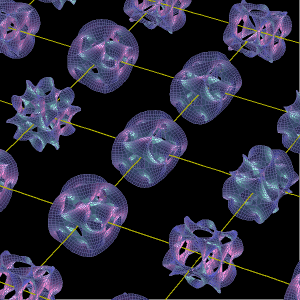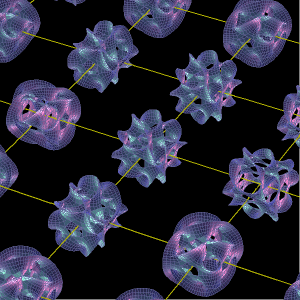


カラビ ヤウ空間を見てみよう とね日記



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ


共振論 第二坑 1 ただ共振だけを感じる サブボディ共振塾 ヒマラヤ



10次元までの世界を段階的に徹底解説 6次元で全宇宙にアクセス 7次元でもう1つの宇宙へ 高次元世界のすべて 17年11月29日 エキサイトニュース



ミラー対称性 弦理論 Wikiwand



日本科学未来館 7月新登場の 未来館 サイエンスtシャツ3種 その1つ カラビ ヤウ多様体 をご紹介 Facebook



Geometry Of Dimension Hidden In String Theory The Form Of The Universe Invisible 12 Isbn Japanese Import Amazon Com Books



15 超弦理論入門講座 カラビ ヤウ空間 Youtube



10次元までの世界を段階的に徹底解説 6次元で全宇宙にアクセス 7次元でもう1つの宇宙へ 高次元世界のすべて 17年11月29日 エキサイトニュース


1



Tatsuki Hayama 巴山竜来 Artworks サイエンス社 数理科学 18年10月号


ドーナツ 銀河 宇宙論 説 輪 カラビ ヤウ多様体 の画像素材 写真素材ならイメージナビ



超弦理論 I 超弦理論とブラックホール Super String Theory And Black Hole 6000万年光年彼方のおとめ座の方向 M87星雲の中心の太陽質量の65億倍の ブラックホール 19年4月に撮影 ブラックホールのイメージ図 ブラックホールの特異点に出現する



4ページ目の 時間考察 Tough Boy World Of Cap Hiro 楽天ブログ


学位論文要旨詳細



カラビ ヤウ空間 竹内薫の はじめての数式処理ソフト より Maxima で綴る数学の旅



見えざる宇宙のかたち シン トゥン ヤウ スティーヴ ネイディス とね日記



標準模型instagram Posts Photos And Videos Picuki Com



Mnpyq Kzmp0gtm


Http Www Icepp S U Tokyo Ac Jp Asai Lhc2 Memo Pdf



整列 物理学 弦理論 カラビ ヤウ多様体 の画像素材 Cg素材ならイメージナビ



カラビ ヤウ空間を見てみよう とね日記



カラビヤウ多様体弦理論におけるスペースの余分次元の構造3 D にはイラストが表示されます 3dのストックフォトや画像を多数ご用意 Istock



アニメ 色づく世界の明日から タイムマシンは カラビ ヤウ Bus 正多面体クラブ



多次元宇宙のうねりが生むインフレーション 日経サイエンス



9次元の世界へようこそ 超弦理論 が映像に 量子力学と相対性理論を統合する 万物の理論 とは 4 5 Jbpress Japan Business Press



Geometry Of Dimension Hidden In String Theory The Form Of The Universe Invisible 12 Isbn Japanese Import Amazon Com Books



カラビ ヤウ多様体 Wikipedia


地震前兆 地震雲 湘南 ikuのサイト Earthquake Omen Observation



Rでカラビ ヤウ多様体を出そうとした Youtube
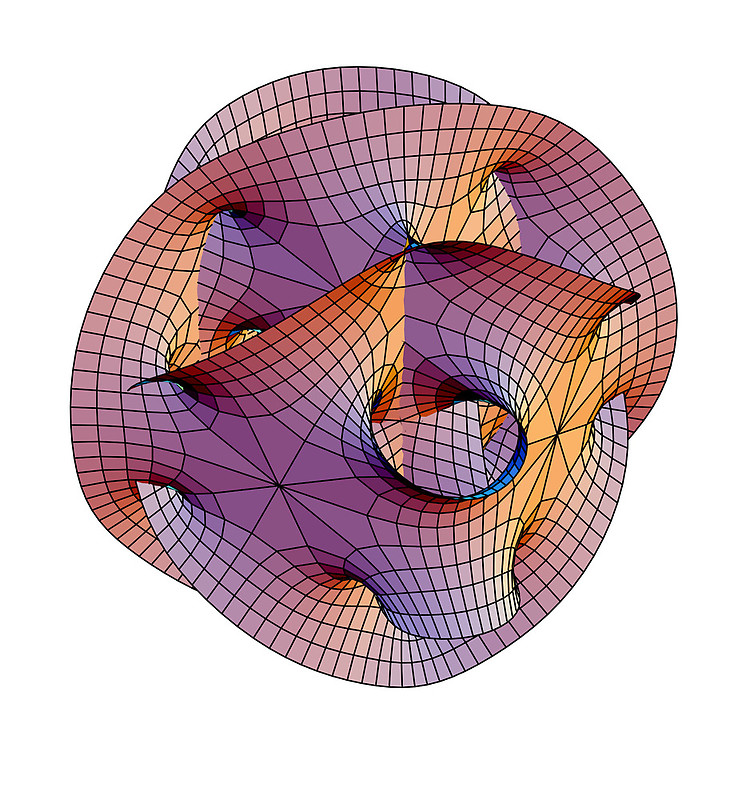


Dr Kakuいわく 神の弦は響く 聖書と超弦理論 Idle Utterance



気ままにひとりごと



Yagokoro Eirin Touhou Drawn By Alison Alison Airlines Danbooru



Calabi Yau多様体をブラウザ上に可視化する Three Js Sw1227 S Diary



今日の科学の美の壺 カラビ ヤウ多様体クリスタル Calabi Yau Manifold Bathsheba Sculpture 正多面体クラブ


Geodiary


整列 物理学 弦理論 カラビ ヤウ多様体 の画像素材 Cg素材ならイメージナビ



カラビ ヤウ空間 Classic音楽 リュート 宇宙



アニメ 色づく世界の明日から タイムマシンは カラビ ヤウ Bus 正多面体クラブ



9次元から来た男とは何者か 9次元からきた男 日本科学未来館


Steam Workshop カラビ ヤウ空間



ミラー対称性 弦理論 Wikiwand



サイエンス社 Di Twitter 新刊 数理科学18年10月号は本日発売です 今回の特集は カラビ ヤウ多様体 その多彩な姿に迫る です カラビ ヤウ多様体の多様な姿を探るべく 数学や物理の各分野の立場から見たカラビ ヤウ多様体について探っていきます


悠々人生のエッセイ カラビ ヤウ多様体



サイエンス社 No Twitter 近刊 次回の数理科学18年10月号 カラビ ヤウ多様体 ができました 発売日は9月日 木 です 数理科学の配本は大型書店や大学生協など限られております ご購入希望のお客様はぜひお近くの書店で予約して頂きますようお願い致し


新着記事一覧 Tough Boy World Of Cap Hiro 楽天ブログ



新着記事一覧 Tough Boy World Of Cap Hiro 楽天ブログ


0 件のコメント:
コメントを投稿